mathematical curiosity (one of those again)
 

OK, so in my probability and statistics class we talked about normal distribution, which is defined by;



where mu is the average (or first moment about the origin) and lowercase sigma is standard deviation (or square root of variance)

This is a probability distribution, so the area under this curve over the entire interval is going to be 1.

OK that's easy peasy, but a while ago I remember stumbling upon this formula.... the Gaussian Integral (not to be confused with Gaussian Distribution)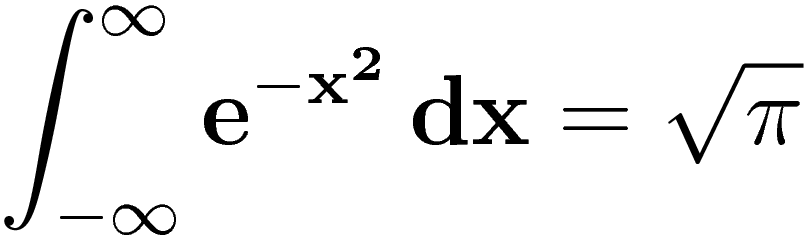



These formulas, for what they are representing are very very similar. They have the same curvature and are over the same interval.

The discrepancy between the two is the computed integrals. The normal distribution will have an area under its curvature of 1 (obviously), and the area under the Gaussian Integral I just presented is the square root of pi. The area of the Gaussian Integral can be easily proved with this method.



so anyway my question......

is there any bridge between these formulas?

Re: mathematical curiosity (one of those again)
 

not sure what question you're asking. are you trying to verify using the gaussian integral formula that the area under the normal distribution curve is indeed 1? if you start with the gaussian integral formula and substitute y = (x - mu)/(sigma*sqrt2) then the normal distribution pdf becomes 1/sqrt(pi)*exp(-y^2) which integrates to 1

let me know if you were asking a different question

Re: mathematical curiosity (one of those again)
 

Are these formulas related.... like could one be written as the other or something... I guess that's what I'm asking

OK THIS is what im asking, could you algebraically manipulate one of those formulas to arrive at the other one or vice versa?

Re: mathematical curiosity (one of those again)
 

The normal distribution function is just a transformation of a Gaussian Function. The variance/mean/etc. all impose characteristics on this function to ensure that the integral is equal to 1.

Zapmeister proved it but not in a detailed line-by-line way like your post did for a base Gaussian Function.

edit:

here is the standard form for a Gaussian Function:

Re: mathematical curiosity (one of those again)
 

yeah I understand that I was just looking for the step by step way of doing it I just couldn't do it on my own and I didn't see one online.

ok dynamo that's all I needed to see question solved idk where you found that that was EXACTLY what I was looking for.....

wow painfully obvious I'm mad at myself for not figuring that out. the curve ball was that the parent function can't really be deduced (at least by me) by looking at e^(-x^2)

Re: mathematical curiosity (one of those again)
 

So if I understand correctly, you just want to derive the Gaussian Integral from the Gaussian Distribution? If that's the case, it's just simply a case of a few substitutions.

I was trying to use LaTeX, but I kept screwing something up, so I wrote it down instead!!! The picture is sort of big though, so I apologise about that.

Re: mathematical curiosity (one of those again)
 

One bit of insight as to how you can know these formulas can be derived from each other without even needing to do any work is knowing the basic relationships of functions and chain rule. For example, these two equations are related the same way you know that f(x) = x^2 is related to g(x) = 3(x-4)^2.

The transformations that turn the Gaussian Integral into the normal distribution are:
- Horizontal translation by a constant, μ (which obviously does not affect the integral given the limits follow the translation)
- Horizontal stretch by a constant factor, σ√2 (which changes the integral by that factor)
- Vertical stretch by a constant factor, 1/σ√(2π) (which changes the integral by that factor)

√π * σ√2 / σ√(2π) = 1

Re: mathematical curiosity (one of those again)
 

thanks

and yes sg i understand how they are derived with translations i wanted to see the work

Re: mathematical curiosity (one of those again)
 

why dont u just ask nick

Re: mathematical curiosity (one of those again)
 

¯\_(ツ)_/¯

Re: mathematical curiosity (one of those again)
 

next time

Re: mathematical curiosity (one of those again)
 

Another fun thing about the normal curve is that the inflection points are located one standard deviation away from the mean/median/mode.

Re: mathematical curiosity (one of those again)
 

Huh.

...

Prove it.

Re: mathematical curiosity (one of those again)
 

Re: mathematical curiosity (one of those again)
 

good read

Re: mathematical curiosity (one of those again)
 

Thanks for the Helping Hand.